 I often receive requests to write in runes an Old Norse word or phrase. People naturally tend to expect that nothing could be easier, since runes were initially created for the Old Norse language. There should be rules as for how to write with runes in that language. There should be some kind of table. However, tables that give Younger Futhark runes along with letters, usually do the opposite: they explain how to transform runes into letters. Those tables are of no use if you are interested in the reverse process.
I often receive requests to write in runes an Old Norse word or phrase. People naturally tend to expect that nothing could be easier, since runes were initially created for the Old Norse language. There should be rules as for how to write with runes in that language. There should be some kind of table. However, tables that give Younger Futhark runes along with letters, usually do the opposite: they explain how to transform runes into letters. Those tables are of no use if you are interested in the reverse process.
Moreover, a mere table would not be enough to write in Old Norse with runes, it takes a whole tutorial to learn how to do that the way it might have been done on a Viking Age runestone ca. AD 1000.
1. Have Your Text in Old Norse
The first step is to make sure your text is in Old Norse. Note that modern Icelandic is very close to Old Norse. Icelanders usually have no difficulty in understanding texts that were written a thousand years ago, because their language changed very little since the time. Also note that a lot of Old Norse texts are available online in modern Icelandic orthography. Thus we have to make sure which of the three possible options we actually have:
- Modern Icelandic text
- Old Norse text in modern Icelandic orthography
- Old Norse text in Old Norse orthography
It is important to know if we want to do the inscription the way it might have been done in the Viking Age. A simple rule of thumb is as follows:
- If you see words ég (‘I’) and og (‘and’), it’s modern Icelandic.
- If you see ek and ok instead, but also words að (‘to’) and það (‘that’), and the letter ö in any word, it’s Old Norse in modern Icelandic orthography.
- If you see ek, ok, at, and þat, and also letters ø or ǫ, it’s Old Norse in Old Norse orthography.
2. Choose Your Version of the Futhark Runic Alphabet
People sometimes want to write in Old Norse with the Elder Futhark runes, simply because they are visually more appealing. Why not. However, the standard runic alphabet for the Viking Age runic inscriptions was the Younger Futhark. It had three variants:
- Long Branch: Danish runes (also often considered as the standard Younger Futhark set).
- Short Twig: Norwegian-Swedish or Rök runes (more minimalistic variant).
- Staveless or Hålsinge runes (triumph of minimalism).
Long Branch runes originated in Denmark but eventually were used more or less throughout Scandinavia (and wherever Vikings pillaged, traded and drank). Staveless runes were used only locally. (By the way, if you wish to emphasize your Norwegian or Swedish descent, I don’t think your choice is limited by the Short Twig option alone.)
3. Discriminate Between the Runes Where Necessary
3.1. Use of either reið or ýr rune for r.
In Proto-Norse and Old Norse (up to a certain time) there were two phonemes for r: /r/ (reið rune) and /R/ (ýr rune). The first one had always been /r/, since the Indo-European times. The second one, /R/, had been /s/ in Indo-European, and then /z/ in Proto-Germanic. Viking Age runic inscriptions differentiate between the two. Old Norse literature written down in the 13th century (and Old Norse orthography, which is based on it) does not. Bad news: we are to know the etymology of the word in order to write it in Viking Age runes correctly. Good news: there is a rule of thumb that covers most cases. It is enough to make an authentic runic inscription, since Viking Age runecarvers were not ideal at differentiating between the two: they often put ýr where reið was needed and vice versa.
Rule of thumb: Nearly any r that is in a case and number ending (for nouns) or in a person and number ending (for regular verbs) is /R/, not /r/.
Examples:
kallar ‘he calls’ (present indicative 3rd person singular) -r < -R < -z

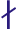
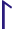
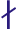
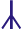
armr ‘hand’ (nominative singular): -r < -aR < -az
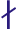
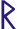

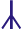
skildir ‘shields’ (nominative plural): -ir < -juR < -juz < -iwiz
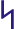

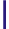
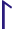
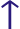
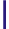
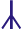
heiðar ‘of the wasteland’ (genitive singular): -ar < -ioR < -ioz

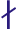
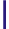

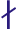
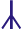
Note, however, that r at the end of the words faðir ‘father’, bróðir ‘brother’, móðir ‘mother’, dóttir ‘daughter’ and systir ‘sister’ belongs to the stem and not the ending, so all these words have reið rune at the end.
The word Thor also has reið, since r + R gave r: Þórr (þur) < Þonar < ÞunraR < Þunraz

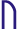
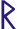
3.2. Use of either ár or ą́ss rune for a.
The rune ą́ss < ansuz was used for a nasalized /ã/, that is for groups an + consonant in standard Old Norse orthography. Example: England was spelt ikląt in runic inscriptions:
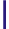

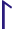
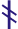
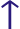
The rune ár was used for a and á in all other positions (but sometimes for /ã/, too).
3.3. Use of either nauð rune or nothing for n; maðr rune or nothing for m
All the other nasalized vowels did not have special runes for them, so whenever you have a group of vowel + n + g, d, render it as vowel + g, d (without nauð rune). Use nauð for n in all other cases. Example: konung was spelt kunukR in runic inscriptions:

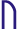

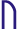

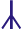
The same applies to groups vowel + m + b: render it as vowel + b (without maðr rune). Use maðr for m in all other cases.
3.4. Use of either fé or úr rune for v.
Before vowels v was spelt with úr rune. Example: viking (in the sense of raid, not person) was spelt uikik in runic inscriptions:
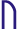
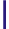

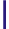

The rune fé was used for v in all other positions.
3.5. Use of either úr or ár + úr for o.
O and ó are usually spelt as úr in runic inscriptions and only occasionally as ár+úr. Note, however, that ok ‘and’ was nearly always spelt auk:
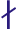
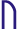

4. Refer to This General Table
Rune variants that go first appear more frequently in the Viking Age runic inscriptions. If there is a reference to a paragraph above, the use of variants depends on a rule.
| a, á | 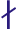 or or 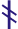 (3.2) (3.2) |
p, b, mb | 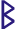 |
| b, mb, p | 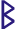 |
r | 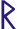 or or 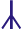 (3.1) (3.1) |
| d, nd, t | 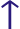 |
s | 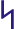 |
| e, é | 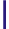 or or 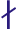 , rarely , rarely
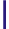 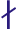 |
t, d, nd | 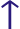 |
| f, v | 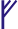 |
u, ú | 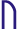 |
| g, ng, k |  |
v | 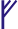 or or 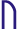 (3.4) (3.4) |
| h |  |
x |
 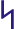 |
| i , í | 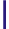 |
y, ý | 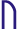 or or 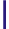 |
| j | 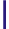 |
z | 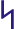 |
| k, g, ng |  |
ø, ǿ (œ) | 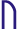 or or 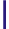 |
| l | 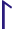 |
ǫ, ǫ́ | 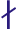 or or 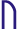 , rarely , rarely
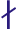 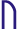 |
| m |  |
æ | 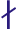 , rarely , rarely 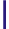 |
| n |  |
ei |
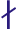 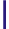 |
| o, ó | 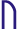 or or
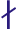 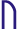 (3.5) (3.5) |
þ, ð |  |
5. Do Not Use Double Runes
Viking Age runic inscriptions normally do not have two identical runes in a row. This is valid even for two runes that belong to two different words, one at the end of a previous one, the other at the beginning of a following one (if no separators are used). Cf. raþu for rað þu below.
6. Use Dots or x Signs as Spaces
Viking Age runic inscriptions either do not have separators between words at all, or use dots, combinations of dots or x signs as separators.
7. (Optional) Begin Your Inscription With a Traditional Formula
Some runestone inscriptions begin with words Rað þu (Interpret!) or Rað þu runar (Interpret the runes!):
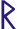
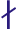

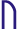

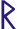
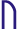

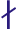
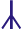
Runic inscription U 29 (Hillersjö stone) has the word raþu in the eye of a dragon (see the image above left).
This tutorial is © copyright. No part of it may be copied or reproduced.

Hello, I’m looking for a true translation for “raven.” Reading through your articles (very good by the way), if I understand it right, start with the Icelandic or Old Norse translation of the word and then convert to runes? So for raven I found “rifinn” in Icelandic and either “hrafn” “hrafna” or “hrefna” for Old Norse. Is one of these correct? Thanks
Hello Dustin. Old Norse for raven is hrafn.
I would like to know if my translation is correct. The basic sentence is:
“til árs ok friðar”
here is the link
https://i82.servimg.com/u/f82/19/42/69/92/til_ar10.jpg
it’s for my thesis so it’s pretty important. Thank you
Hello. Yes, it’s correct.
Thank you!
Congratulations for this site.
It is excellent.
I wanted to translate some old Norse words to younger futhark long branch. Could you let me know if I did it correctly and if not please explain where I went wrong so that I may learn even more.
ᛅᛋᚴᛅᚱᚦᛦ Asgardr
ᛅᛚᚠᚼᛅᛁᛘᛦ Alfheimr
ᛁᚢᛏᚢᚾᚼᛅᛁᛘᛦ Jotunheimr
ᛘᚢᛋᛒᛅᛚᚼᛅᛁᛘᛦ Muspelheimr
If I understood the rules correctly how can I go about going into elder futhark?
Ásgarðr is incorrect as the first rune should be an áss ᚬ because the á is nasalized (since it comes from proto-Norse *ansaz).
Álfheimr looks correct to me.
Jǫtunheimr is wrong since the ǫ is a u-umlauted a and is therefore represented by ár ᛅ.
Múspellsheimr is also incorrect since you’re missing the final -s from Múspells- (a genitive case ending to glue the compound word together) and the e is probably not an i-umlauted a so it’s probably not represented by ár ᛅ but íss ᛁ. ‘Probably’ because no one really knows what the word means and its etymology is uncertain.
Hi There!
im trying to translate the word Brotherhood into Long branch, but im slightly confused by the not using double runes, do you just use the one or use another to signify a double letter? kinda want to get it 100% right as its a tattoo design
Any help would be amazing as i have been looking forward to this for a long time :)
Hello Scott. Old Norse for brotherhood is bróðerni. It has no double letters.
Hello, I am very lost in 3.1., what is the rule for using /r/ and /R/ for adjectives (I am trying to write máttugr, þróttigr, verðr specifically) ? Thank you.
Hello Lucy. All these words have final -r < -R < -z.
Hi.
I’m interested in doing a runic tattoo from the poetic Edda “Fáfnismál” stanza 16, which goes:
Ægishjalm
bar ek of alda sonum,
meðan ek of menjum lák;
einn rammari
hugðumk öllum vera,
fannk-a ek svá marga mögu.
I understand that it is in Old Norse but, despite reading the tutorial, I have encountered some difficulties to translate into the Long Branch Young Futhark, as recommended. Can you help me?
Thanks!
How can I help you, Bruno?
I’ve followed your instructions as described above, plus I used a font named Gullskoen (that I’ve found here: https://folk.uib.no/hnooh/runefont/Gullskoen-e.html – ) to help me out with the runes, and came up with this result: https://www.dropbox.com/s/zpy223zr311y7mi/runa.png
I want to know if you have some tips on the writing that I did or corrections, if necessary
Thanks for your help!
Bruno, a lot of mistakes. It should be entirely rewritten.
Hi,
Your website is fabulous.
I am going to engrave a stone with my family name, which is a place name in Norway: Mannsåker. I know from the tutorial not to use a double N but how would you recommend differentiating betweeen the first a and the a with the circle over it? Would you apply rule 3.2? Thanks in advance.
Hello. Yes, I would apply 3.2 using ą́ss and a single nauð rune. As for the letter å, I would use the same rune as for a, since Norwegian åker is from Old Norse akr.
I’m glad you liked the website.
Hi!
I’ve used your guide and I wonder if you could check over if I did it correctly. Also help where I was lost. I have ADD so doing this was very hard but I did my best in trying to understand the guide.
‘Trail of blood upon ground leads the traveler to heart and home.’
I had it translated to modern Icelandic.
‘Blóðslóð á jörðu leiðir ferðamanninn til hjarta og heim.’
Then I used the Short Twig runes.
https://imgur.com/a/8m3MTcc
Some words I could not find the runes for so I marked them with ? and with the letter underneath. In this case Ö and G.
Thanks!
Hello Jennifer. The translation is into modern Icelandic. It is okay, since it is very close to Old Norse, but haven’t you used Google Translate or a similar machine translation tool, have you? I am asking because it doesn’t seem grammatically correct (which is typical for machine translation). The best way would be to ask someone who studied Old Norse or modern Icelandic or else a native speaker of Icelandic to do that. Then I will help you to write the phrase with runes. Feel free to leave a comment here. I sometimes answer weeks after people post questions here, but the reason is not I don’t care, it’s because my work does not leave a lot of free time for this project.
Hi i am trying to find the proper runes for the spelling of brotherhood but using old Norse “bræðralag” if I could get some assistance that would be greatly appreciated. I keep coming up with double rune so I think I’m doing something wrong.
Do you have any difficulty to apply the rules set in the tutorial above?
i am following the tutorial but i feel i may have misunderstood some thing as i get the following:
berkana raido raido ansuz laguz ansuz gebo
You may get this result if you use the converter. Follow the tutorial instead.
Dear vikingrune.com,
First of all, I love your website! I would like to transcribe the old Norse word “metnaðr” from the 79th verse of the Hávamál into younger futhark. I have come to the following: ᛉᛁᛏᚾᛅᚦᛣ. Is that correct? I’m not sure whether to use reið or ýr.
Hello Björn. That’s correct.